BST与AVL与RBT

导语

BST（二叉排序树、二叉搜索树、二叉查找树），AVL（平衡二叉树）以及BRT（红黑树）是非常重要的数据结构。

BST

BST性质

BST的中文名很多，实际上都是一个东西。

• 在二叉树中的第i层上至多有$2^{i-1}$个结点（i>=1)。
• 深度为k的二叉树至多有$2^k-1$个节点（k>=1)。
• 对任何一棵二叉树T，如果其叶结点数目为$n_0$，度为2的节点数目为$n_2$，则$n_0$=+1。
• 具有n个节点的完全二叉树的深度为$log_{2}{n}+1$

BST操作

查找、插入、删除、遍历操作（比较简单）

#include<stdio.h>
#include<stdlib.h>
/*
	二叉排序树  <==> 二叉搜索树 (BST) <==>  二叉查找树 

	1. 二叉排序树的查找功能 (递归、非递归实现)    --> 查找效率很大程度上取决于二叉排序树的高度。 
	2. 二叉排序树的插入功能 (默认不同元素的值才插入) --> 先查找再插入 
	3. 二叉排序树的删除功能 (两种实现方式, 1.后继结点顶上来，删除后继结点 2.前驱结点顶上来,删除前驱结点)  --> 先查找再删除 
	4. 根据一个序列,构造二叉排序树的功能。  --> 其实就是遍历序列 插入二叉排序树。 

	二叉排序树的一个重要指标 : 平均查找长度(ASL)
		平均查找长度又分: 查找成功的平均查找长度    sum(查找每个元素的比较次数)/元素个数  
						  查找失败的平均查找长度    sum(查找每个失败元素时比较次数)/失败出现的可能数 
  		结论: 二叉排序树最好尽可能平衡,因为这样的查找效率可以达到O(log n).  
		 


*/ 
#define ElemType int
#define null NULL
typedef struct BSTNode{
	ElemType key;
	struct BSTNode *lchild,*rchild;
}BSTNode;
 
//二叉搜索树查找功能的非递归实现   时间复杂度O(log n) - O(n) 
BSTNode* findKey(BSTNode *t,ElemType value){ //最坏空间复杂度O(1) 
	//t == null 代表查找元素不存在   
	while(t != null && value != t->key){
		if(t->key > value){
			t = t->lchild;
		}else{
			t = t->rchild;
		}
	}
	return t;
}
//二叉搜索树的查找功能(递归实现)
BSTNode* findKey2(BSTNode *t, ElemType value){ //最坏空间复杂度O(h)  h是二叉搜索树的最大高度。 
	if(t == null){
		return null;
	}
	if(t->key == value){
		return t;
	}
	if(t->key > value){
		return findKey2(t->lchild,value);
	}else{
		return findKey2(t->rchild,value);
	}
} 
 
//二叉搜索树的插入功能 (默认不同元素的值才插入) 
bool BST_insert(BSTNode **t, ElemType value){
	//插入第一个结点 
	if(*t == null){
		BSTNode *s = (BSTNode *)malloc(sizeof(BSTNode));
		s->key = value;
		s->lchild = null;
		s->rchild = null;
	 	*t=s;
		return true; 		 
	}
	if(((*t)->key == value)){
		return false;
	}else if((*t)->key > value && (*t)->lchild == null){
		BSTNode *s = (BSTNode *)malloc(sizeof(BSTNode));
		s->key = value;
		s->lchild = null;
		s->rchild = null;
		(*t)->lchild=s;
		return true; 
	}else if((*t)->key < value && (*t)->rchild == null){
		BSTNode *s = (BSTNode *)malloc(sizeof(BSTNode));
		s->key = value;
		s->lchild = null;
		s->rchild = null;
		(*t)->rchild=s;
		return true; 
	}else{
		//递归寻找
		if((*t)->key > value){
	 		BST_insert(&((*t)->lchild),value);
		}else{
	 		BST_insert(&((*t)->rchild),value);
		}
	}
} 
//根据序列构造二叉搜索树
BSTNode* Creat_BST(ElemType str[],int n){
	BSTNode *t = null;  //初始时t为空树 
	for(int i = 0;i < n;i++){  //依次将每个关键字插入到二叉排序树中 
	
		BST_insert(&t,str[i]);
	
	}
	return t;
}
 
//二叉搜索树的删除功能
/*
	1.删除的结点是叶子结点
	2.删除的结点只有左子树或者只有右子树 
	3.删除的结点既有左子树又有右子树 
*/
//value是要删除的元素值
//不应该找到要删除的元素,而是应该找到要删除元素的前一个元素。 
BSTNode* BST_delete(BSTNode *b,ElemType	value){
	BSTNode *t = b; 
	//f指针指向的是要删除结点的双亲 
	BSTNode *f = null;
	//判断t是f的哪个孩子(左孩子 or 右孩子) 
	int child = 0;
	while(t != null && t->key != value ){
		f=t; 
		if(t->key > value){
			child = -1;
			t= t->lchild;
		}else{
			child = 1;
			t=t->rchild;
		}
	}

	//没找到  删除失败 
	if(t == null){
		return b; 
	}

	 //删除的是根节点,并且左右子树都没有 
	 if(f == null && t -> rchild == null && t->lchild == null ){
	 	b = null;
	 	free(t);
 		return b;
 	}
 	//删除的是根节点,并且没有左子树,只有右子树 
	if(f == null && t->lchild == null && t->rchild	!= null){
		b=t->rchild;
		free(t);
		return b;
	}

	//删除的是根节点,并且没有右子树,只有左子树 
	if(f == null && t->rchild == null && t->lchild	!= null){
		b=t->lchild;
		free(t);
		return b;
	}


	//删除的是叶子结点 
	if(t->lchild == null && t->rchild == null){
		free(t);
		//删除的结点是他爹的左孩子
		if(child == -1){
			f->lchild = null; 
		}
		if(child == 1){
			f->rchild = null;
		}
		return b; 	
	}
	//删除的结点只有右子树,没有左子树 
	 if(t->lchild == null && t->rchild != null){
	 	//删除的结点是他爹的左孩子
 		if(child == -1){
		 	f->lchild = t->rchild;
		 	free(t);
	 	}
	 	if(child == 1){
	 		f->rchild = t->rchild;
			free(t); 
	 	}
	 	return b;
 	}
	  
	//删除的结点只有左子树,没有右子树 
	if(t->lchild != null && t->rchild == null){
		//删除的结点是他爹的左孩子 
 		if(child == -1){
		 	f->lchild = t->lchild;
		 	free(t);
	 	}
	 	if(child == 1){
	 		f->rchild = t->lchild;
			free(t); 
	 	}
	 	return b;
	} 
	//删除的结点既有左子树又有右子树 
	if(t->lchild != null && t->rchild != null ){
		//两种方式解决  1.将右子树中最小的元素放到此位置,并删除右子树中的最小元素。 
		//              2.将左子树中最大的元素放到此位置,并删除左子树中的最大元素。
		//方式1代码 
		//右子树中最小的元素,就是右子树中最左下角的元素.
	//	BSTNode *q = t->rchild;
	//	while(q->lchild != null ){
	//		q = q->lchild;
	//	
	//	}
		//q即为要查找的右子树的最小元素
	//1
		// ElemType temp = q->key;
		 //右子树中删除值最小的元素 , 先删除再赋值 
		 //BST_delete(b,q->key);
		 //t->key = temp;
	//2	 巧妙的利用了返回值,无缝将右子树部分删除掉q并衔接。 
     //    t->key = q->key; 
	   //  t->rchild = BST_delete(t->rchild,q->key);	 
		 
		//方式2代码 
		//左子树中最大的元素,就是左子树中最右下角的元素。 
	
		BSTNode *z = t->lchild;
		while(z->rchild != null){
			z = z->rchild;
		} 
		//z即为要查找的左子树的最大元素
		t->key = z->key;
		t->lchild = BST_delete(t->lchild,z->key); 
		return b;
	} 
}
 
 
 
 

//二叉树的中序遍历
void in_order(BSTNode *t){
	if(t != null){
		in_order(t->lchild);
		printf("%d ",t->key);
		in_order(t->rchild);
	}
}
 
int main(int argc, char *argv[])
{
	ElemType str[] = {19,13,11,8,50,66,70,60,63,61,65,26,30,21};
	BSTNode *m = Creat_BST(str,14);
	in_order(m);
	printf("\n");
	BSTNode *end = BST_delete(m,70); 
	printf("\n");
	in_order(end);
	return 0;
}

AVL

AVL性质

1. AVL的左右子树都是AVL树
2. AVL左右子树高度之差的绝对值不超过1

AVL操作

为了让AVL在操作之后仍抱有AVL的性质，AVL的增删查改操作相较于BST增加了一些难度，但也只是一些罢了，不过是左旋、右旋操作罢了

#include<stack>
#include<iostream>
using namespace std;

template<class K,class V>
struct AVLNode
{
    AVLNode<K, V> * _pLeft;
    AVLNode<K, V> * _pRight;
    K key;
    V value;
    int bf;

    AVLNode()
        :_pLeft(NULL)
        , _pRight(NULL)
    {}

    AVLNode(const K key, const V value)
        :_pLeft(NULL)
        , _pRight(NULL)
        , key(key)
        , value(value)
        , bf(0)
    {}

};


template<class K,class V>
class AVLTree
{
    //typedef AVLNode<class K, class V> Node;
    //typedef AVLNode<class K, class V> * PNode;

public:
    // 构造函数--无参
    AVLTree()
        :_pRoot(NULL)
    {}

    ////构造函函数--含参
    //AVLTree(const K key, const V value)

    //{}

    // 插入函数
    bool Insert(const K key, const V value)
    {
        return _Insert(key, value, _pRoot);
    }

    // 显示函数
    void showTree()
    {
        _showTree(_pRoot);
    }
    // 删除函数
    bool Remove(K key)
    {
        return Remove(_pRoot, key);
    }



private:
    AVLNode<K, V> * _pRoot;

    // 插入函数
    bool _Insert(const K key, const V value, AVLNode<K, V> *& ptr)
    {
        AVLNode<K, V> * pCur = ptr;
        AVLNode<K, V> *& pParent = _pRoot; // ???????????????????????????????????????????
        stack<AVLNode<K, V> *> s;
        while (pCur != NULL)
        {
            if (pCur->key == key)
                return false;

            pParent = pCur;
            s.push(pParent);
            if (pCur->key > key)
            {
                pCur = pCur->_pLeft;
            }
            else if (pCur->key < key)
            {
                pCur = pCur->_pRight;
            }
        }
        // 所插位置为NULL 新建结点
        pCur = new AVLNode<K, V>(key, value);
        if (pCur == NULL)
        {
            cerr << "存储空间不足！" << endl;
            exit(1);
        }

        // 判断是否为空树
        if (pParent == NULL)
        {
            ptr = pCur;
            return true;
        }
        if (key < pParent->key)
            pParent->_pLeft = pCur;
        else
            pParent->_pRight = pCur;

        // 调整平衡
        while (s.empty() == false)
        {
            pParent = s.top();
            s.pop();
            if (pCur == pParent->_pLeft)
                pParent->bf--;
            else
                pParent->bf++;

            if (pParent->bf == 0)
                break;
            if (pParent->bf == 1 || pParent->bf == -1)
                pCur = pParent;
            if (pParent->bf == 2 || pParent->bf == -2)
            {
                // 进行调整
                int d;// 调整平衡因子
                d = (pParent->bf < 0) ? -1 : 1;
                if (pCur->bf == d)
                {
                    if (d == -1)
                        RotateR(pParent); // 右单旋
                    else
                        RotateL(pParent); // 左单旋
                }
                else
                {
                    if (d == -1)
                        RotateLR(pParent); // 左右双旋
                    else
                        RotateRL(pParent); // 右左双旋
                }
                break;
            }
            if (s.empty() == true)
                pCur = pParent;
            else
            {
                AVLNode<K, V> * q;
                q = s.top();
                if (q->key > pParent->key)
                    q->_pLeft = pParent;
                else
                    q->_pRight = pParent;
            }
        }
        return true;
    }

    // 左单旋
    void RotateL(AVLNode<K, V> *& ptr)
    {
        // 右子树比左子树高
        // 对以ptr为根的AVL树作左单旋转，旋转后新根在ptr
        AVLNode<K, V> * subL = ptr; // 要左旋的结点
        ptr = subL->_pRight;

        subL->_pRight = ptr->_pLeft;
        ptr->_pLeft = subL;
        ptr->bf = subL->bf = 0;
    }

    // 右单旋
    void RotateR(AVLNode<K, V> *& ptr)
    {
        // 左子树比右子树高
        AVLNode<K, V> * subR = ptr; // 要右旋的结点
        ptr = ptr->_pLeft;

        subR->_pLeft = ptr->_pRight;
        ptr->_pRight = subR;
        ptr->bf = subR->bf = 0;
    }

    // 先左再右单旋
    void RotateLR(AVLNode<K, V> *& ptr)
    {
        AVLNode<K, V> * subL = ptr->_pLeft;
        AVLNode<K, V> * subR = ptr;

        ptr = subL->_pRight;
        subL->_pRight = ptr->_pLeft;
        ptr->_pLeft = subL;

        if (ptr->bf < 0)
        {
            subL->bf = 0;
        }
        else
            subL->bf = -1;

        subR->_pLeft = ptr->_pRight;
        ptr->_pRight = subR;

        if (ptr->bf == -1)
            subR->bf = 1;
        else
            subR->bf = 0;

        ptr->bf = 0;
    }

    // 先右后左旋转
    void RotateRL(AVLNode<K, V> *& ptr)
    {
        AVLNode<K, V> * subL = ptr;
        AVLNode<K, V> * subR = ptr->_pRight;
        ptr = ptr->_pLeft;

        subR->_pLeft = ptr->_pRight;
        ptr->_pRight = subR;
        if (ptr->bf >= 0)
            subR->bf = 0;
        else
            subR->bf = 1;

        subL->_pRight = ptr->_pLeft;
        ptr->_pLeft = subL;
        if (ptr->bf == 1)
            subL->bf = -1;
        else
            subL->bf = 0;

        ptr->bf = 0;
    }

    // 显示函数
    void _showTree(AVLNode<K, V> * ptr)
    {
        if (ptr == NULL)
            return;
        _showTree(ptr->_pLeft);
        cout << ptr->key << " ";
        _showTree(ptr->_pRight);
    }

    // 删除结点
    bool Remove(AVLNode<K, V> *& ptr, K key)
    {
        AVLNode<K, V> * pCur = ptr;
        AVLNode<K, V> * pParent = ptr;
        AVLNode<K, V> * gParent = NULL;
        AVLNode<K, V> * q; // 左右子树均存在时，找左子树的右结点
        stack<AVLNode<K, V> *> s;
        int pd = 0;
        int gd = 0;
        // 找到须要被删除的结点，将路径上的结点记录在栈中
        while (pCur != NULL)
        {
            if (key == pCur->key)
                break;
            pParent = pCur;
            s.push(pParent);
            if (key > pCur->key)
                pCur = pCur->_pRight;
            else
                pCur = pCur->_pLeft;

        }
        if (pCur == NULL)
            return false;

        if (pCur->_pLeft != NULL && pCur->_pRight != NULL)
        {
            pParent = pCur;
            s.push(pParent);
            q = pCur->_pLeft;
            while (q->_pRight != NULL)
            {
                pParent = q;
                s.push(pParent);
                q = q->_pRight;
            }
            pCur->key = q->key;
            pCur = q;
        }

        // 被删除结点pCur只有一个子结点
        if (pCur->_pLeft != NULL)
            q = pCur->_pLeft;
        else
            q = pCur->_pRight;
        if (pParent == NULL)
            ptr = q;
        else
        {
            if (pParent->_pLeft = pCur)
                pParent->_pLeft = q;
            else
                pParent->_pRight = q;
            // 从新平衡化
            while (s.empty() == false)
            {
                pParent = s.top();
                s.pop();
                if (pParent->_pLeft = pCur)
                    pParent->bf++;
                else
                    pParent->bf--;
                if (s.empty() == false)
                {
                    gParent = s.top();
                    gd = (gParent->_pLeft == pParent) ? -1 : 1;

                }
                else gd = 0;
                if (pParent->bf == 1 || pParent->bf == -1)
                    break;
                if (pParent->_pLeft != 0)
                {
                    if (pParent->bf < 0)
                    {
                        pd = -1;
                        pCur = pParent->_pLeft;
                    }
                    else
                    {
                        pd = 1;
                        pCur = pParent->_pRight;
                    }
                    if (pCur->bf == 0)
                    {
                        if (pd == -1)
                        {
                            RotateR(pParent);
                            pParent->bf = 1;
                            pParent->_pLeft->bf = -1;
                        }
                        else
                        {
                            RotateL(pParent);
                            pParent->bf = -1;
                            pParent->_pRight->bf = 1;
                        }
                        break;
                    }
                    if (q->bf == pd)
                    {
                        if (pd == -1)
                            RotateR(pParent);
                        else
                            RotateL(pParent);
                    }
                    else
                    {
                        if (pd == -1)
                            RotateLR(pParent);
                        else
                            RotateRL(pParent);
                    }
                    if (gd == -1)
                        gParent->_pLeft = pParent;
                    else if (gd == 1)
                        gParent->_pRight = pParent;
                }
                q = pParent;
            }
            if (s.empty() == true)
                ptr = pParent;
        }
        delete pCur;
        return true;
    }
};

int main()
{
    AVLTree<int, int> t;
    t.Insert(1, 11);
    t.Insert(2, 12);
    t.Insert(3, 13);
    t.Insert(4, 14);
    t.showTree();
    t.Remove(2);
    return 0;
}

RBT

RBT性质

1.每个结点要么是红的要么是黑的。

2.根结点是黑的。

3.每个叶结点（叶结点即指树尾端NIL指针或NULL结点）都是黑的。

4.如果一个结点是红的，那么它的两个儿子都是黑的。

5.对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。

借王道一个口诀 左根右，根叶黑，不红红，黑路同

RBT操作

红黑树的5条性质，使一棵n个结点的红黑树始终保持了logn的高度。同时，在进行增删改之后这些性质并不容易被破坏。同时破坏了性质之后的修改也并不复杂。

增

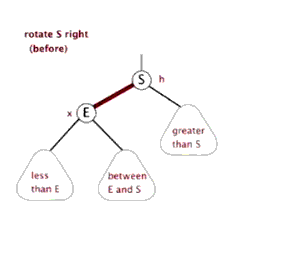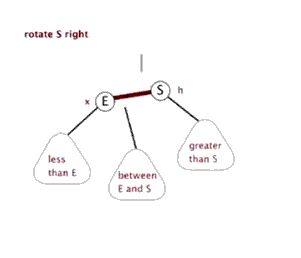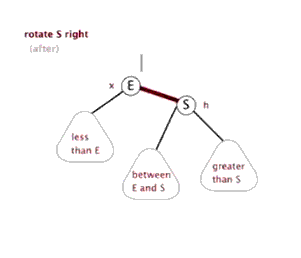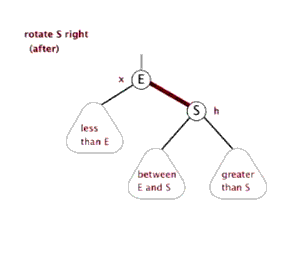
#include<stdafx.h>
#include<malloc.h>
#include <assert.h>

//红黑树
typedef enum ColorType {RED, BLACK} ColorType;
typedef struct rbt_t{
    int key;
    rbt_t * left;
    rbt_t * right;
    rbt_t * p;
    ColorType color;
}rbt_t;

typedef struct rbt_root_t{
    rbt_t* root;
    rbt_t* nil;
}rbt_root_t;

//函数声明
rbt_root_t* rbt_init(void);
static void rbt_handleReorient(rbt_root_t* T, rbt_t* x, int k);
rbt_root_t* rbt_insert(rbt_root_t* &T, int k);
rbt_root_t* rbt_delete(rbt_root_t* &T, int k);

void rbt_transplant(rbt_root_t* T, rbt_t* u, rbt_t* v);

static void rbt_left_rotate( rbt_root_t* T, rbt_t* x);
static void rbt_right_rotate( rbt_root_t* T, rbt_t* x);

void rbt_inPrint(const rbt_root_t* T, rbt_t* t);
void rbt_prePrint(const rbt_t * T, rbt_t* t);
void rbt_print(const rbt_root_t* T);

static rbt_t* rbt_findMin(rbt_root_t * T, rbt_t* t);
static rbt_t* rbt_findMax(rbt_root_t * T, rbt_t* t);

static rbt_t* rbt_findMin(rbt_root_t * T, rbt_t* t){
    if(t == T->nil) return T->nil;

    while(t->left != T->nil)
        t = t->left;
    return t;
}
static rbt_t* rbt_findMax(rbt_root_t * T, rbt_t* t){
    if(t == T->nil) return T->nil;

    while(t->right != T->nil)
        t = t->right;
    return t;
}
/*
*@brief rbt_init 初始化
*/
rbt_root_t* rbt_init(void){
    rbt_root_t* T;

    T = (rbt_root_t*)malloc(sizeof(rbt_root_t));
    assert( NULL != T);

    T->nil = (rbt_t*)malloc(sizeof(rbt_t));
    assert(NULL != T->nil);
    T->nil->color = BLACK;
    T->nil->left = T->nil->right = NULL;
    T->nil->p = NULL;

    T->root = T->nil;

    return T;
}

/*
*@brief rbt_handleReorient  内部函数 由rbt_insert调用
*      在两种情况下调用这个函数：
* 1 x有连个红色儿子
* 2 x为新插入的结点
*
*/ 
void rbt_handleReorient(rbt_root_t* T, rbt_t* x, int k){

    //在第一种情况下，进行颜色翻转； 在第二种情况下，相当于对新插入的x点初始化
    x->color = RED;
    x->left->color = x->right->color = BLACK;

    //如果x.p为红色，那么x.p一定不是根，x.p.p一定不是T.nil，而且为黑色
    if(  RED == x->p->color){
        x->p->p->color = RED;//此时x, p, x.p.p都为红

        if(x->p->key < x->p->p->key){
            if(k > x->p->key){
                x->color = BLACK;//小心地处理颜色
                rbt_left_rotate(T,x->p);
                rbt_right_rotate(T,x->p);
            }else{
                x->p->color = BLACK;//小心地处理颜色
                rbt_right_rotate(T,x->p->p);
            }

        }else{
            if(k < x->p->key){
                x->color = BLACK;
                rbt_right_rotate(T,x->p);
                rbt_left_rotate(T,x->p);
            }else{
                x->p->color = BLACK;
                rbt_left_rotate(T,x->p->p);
            }

        }
    }

    T->root->color = BLACK;//无条件令根为黑色
}
/*
*@brief brt_insert 插入
*1 新插入的结点一定是红色的，如果是黑色的，会破坏条件4（每个结点到null叶结点的每条路径有同样数目的黑色结点）
*2 如果新插入的结点的父亲是黑色的，那么插入完成。 如果父亲是红色的，那么做一个旋转即可。（前提是叔叔是黑色的）
*3 我们这个插入要保证其叔叔是黑色的。也就是在x下沉过程中，不允许存在两个红色结点肩并肩。
*/
rbt_root_t* rbt_insert(rbt_root_t* &T, int k){

    rbt_t * x, *p;
    x = T->root;
    p = x;

    //令x下沉到叶子上，而且保证一路上不会有同时为红色的兄弟
    while( x != T->nil){  
        //
        //保证没有一对兄弟同时为红色， 为什么要这么做？
        if(x != T->nil)   
            if(x->left->color == RED && x->right->color == RED)
                rbt_handleReorient(T,x,k);

        p = x;
        if(k<x->key)
            x = x->left;
        else if(k>x->key)
            x = x->right;
        else{
            printf("\n%d已存在\n",k);
            return T;
        }

    }

    //为x分配空间，并对其进行初始化
    x = (rbt_t *)malloc(sizeof(rbt_t));
    assert(NULL != x);
    x->key = k;
    x->color = RED;
    x->left = x->right = T->nil;
    x->p = p;

    //让x的父亲指向x
    if(T->root == T->nil)
        T->root = x;  
    else if(k < p->key)
        p->left = x;
    else
        p->right = x;

    //因为一路下来，如果x的父亲是红色，那么x的叔叔肯定不是红色了，这个时候只需要做一下翻转即可。
    rbt_handleReorient(T,x,k);

    return T;
}
void rbt_transplant(rbt_root_t* T, rbt_t* u, rbt_t* v){
    if(u->p == T->nil)
        T->root = v;
    else if(u == u->p->left)
        u->p->left =v;
    else
        u->p->right = v;
    v->p = u->p;
}
/*
*@brief rbt_delete 从树中删除 k
*
*
*/
rbt_root_t* rbt_delete(rbt_root_t* &T, int k){
    assert(T != NULL);
    if(NULL == T->root) return T;

    //找到要被删除的叶子结点
    rbt_t * toDelete = T->root; 
    rbt_t * x;

    //找到值为k的结点
    while(toDelete != T->nil && toDelete->key != k){
        if(k<toDelete->key)
            toDelete = toDelete->left;
        else if(k>toDelete->key)
            toDelete = toDelete->right;
    }

    if(toDelete == T->nil){
        printf("\n%d 不存在\n",k);
        return T;
    }


    //如果两个孩子，就找到右子树中最小的代替, alternative最多有一个右孩子
    if(toDelete->left != T->nil && toDelete->right != T->nil){
        rbt_t* alternative = rbt_findMin(T, toDelete->right);
        k = toDelete->key = alternative->key;
        toDelete = alternative;
    }

    if(toDelete->left == T->nil){
        x = toDelete->right;
        rbt_transplant(T,toDelete,toDelete->right);
    }else if(toDelete->right == T->nil){
        x = toDelete->left;
        rbt_transplant(T,toDelete,toDelete->left);
    }



    if(toDelete->color == BLACK){
        //x不是todelete，而是用于代替x的那个
        //如果x颜色为红色的，把x涂成黑色即可， 否则 从根到x处少了一个黑色结点，导致不平衡
        while(x != T->root && x->color == BLACK){
            if(x == x->p->left){
                rbt_t* w = x->p->right;

                //情况1 x的兄弟是红色的，通过
                if(RED == w->color){
                    w->color = BLACK;
                    w->p->color = RED;
                    rbt_left_rotate(T,x->p);
                    w = x->p->right;
                }//处理完情况1之后，w.color== BLACK ， 情况就变成2 3 4 了

                //情况2 x的兄弟是黑色的，并且其儿子都是黑色的。
                if(w->left->color == BLACK && w->right->color == BLACK){
                    if(x->p->color == RED){
                        x->p->color = BLACK;
                        w->color = RED;

                        break;
                    }else{
                        w->color = RED;
                        x = x->p;//x.p左右是平衡的，但是x.p处少了一个黑结点，所以把x.p作为新的x继续循环
                        continue;
                    }
                }

                //情况3 w为黑色的，左孩子为红色。（走到这一步，说明w左右不同时为黑色。）
                if(w->right->color == BLACK){
                    w->left->color = BLACK;
                    w->color = RED;
                    rbt_right_rotate(T,w);
                    w = x->p->right;
                }//处理完之后，变成情况4

                //情况4 走到这一步说明w为黑色， w的左孩子为黑色， 右孩子为红色。

                w->color=x->p->color;
                x->p->color=BLACK;
                w->right->color=BLACK;
                rbt_left_rotate(T,x->p);
                x = T->root;
            }else{
                rbt_t* w = x->p->left;
                //1
                if(w->color == RED){
                    w->color = BLACK;
                    x->p->color = RED;
                    rbt_right_rotate(T,x->p);
                    w = x->p->left;
                }
                //2
                if(w->left->color==BLACK && w->right->color == BLACK){
                    if(x->p->color == RED){
                        x->p->color = BLACK;
                        w->color = RED;
                        break;
                    }else{
                        x->p->color = BLACK;
                        w->color = RED;
                        x = x->p;
                        continue;
                    }
                }

                //3
                if(w->left->color == BLACK){
                    w->color = RED;
                    w->right->color = BLACK;
                    w = x->p->left;
                }

                //4
                w->color=w->p->color;
                x->p->color = BLACK;
                w->left->color = BLACK;
                rbt_right_rotate(T,x->p);
                x = T->root;
            }


        }
        x->color = BLACK;
    }


    //放心删除todelete 吧
    free(toDelete);

    return T;
}


/*
*@brief rbt_left_rotate
*@param[in] T 树根
*@param[in] x 要进行旋转的结点
*/
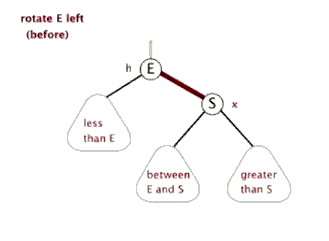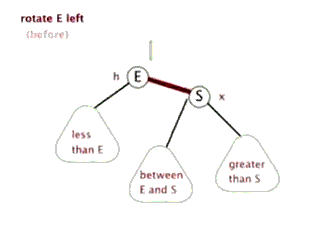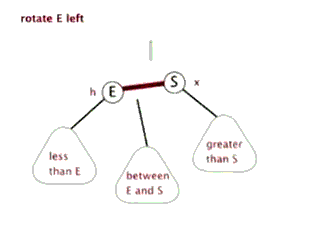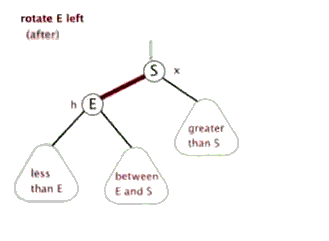
void rbt_left_rotate( rbt_root_t* T, rbt_t* x){
    rbt_t* y = x->right;

    x->right = y->left;
    if(x->right != T->nil)
        x->right->p = x;



    y->p = x->p;
    if(y->p == T->nil){
        T->root = y;
    }else if(y->key < y->p->key)
        y->p->left = y;
    else
        y->p->right = y;

    y->left = x;
    x->p = y;
}
/*
*@brief rbt_right_rotate
*@param[in] 树根
*@param[in] 要进行旋转的结点
*/
void rbt_right_rotate( rbt_root_t* T, rbt_t* x){
    rbt_t * y = x->left;
    x->left = y->right;

    if(T->nil != x->left)
        x->left->p = x;



    y->p = x->p;
    if(y->p == T->nil)
        T->root = y;
    else if(y->key < y->p->key)
        y->p->left= y;
    else
        y->p->right = y;

    y->right = x;
    x->p = y;
}
void rbt_prePrint(const rbt_root_t* T, rbt_t* t){
    if(T->nil == t)return ;
    if(t->color == RED)
        printf("%3dR",t->key);
    else
        printf("%3dB",t->key);
    rbt_prePrint(T,t->left);
    rbt_prePrint(T,t->right);
}
void rbt_inPrint(const rbt_root_t* T, rbt_t* t){
    if(T->nil == t)return ;
    rbt_inPrint(T,t->left);
    if(t->color == RED)
        printf("%3dR",t->key);
    else
        printf("%3dB",t->key);
    rbt_inPrint(T,t->right);
}

//打印程序包括前序遍历和中序遍历两个，因为它俩可以唯一确定一棵二叉树
void rbt_print(const rbt_root_t* T){
    assert(T!=NULL);
    printf("\n前序遍历 ：");
    rbt_prePrint(T,T->root);
    printf("\n中序遍历 ：");
    rbt_inPrint(T,T->root);
    printf("\n");
}

void rbt_test(){
    rbt_root_t* T = rbt_init();

    /************************************************************************/
    /* 1    测试插入
    /*
    /*
    /*输出  前序遍历 ：  7B  2R  1B  5B  4R 11R  8B 14B 15R
    /*      中序遍历 ：  1B  2R  4R  5B  7B  8B 11R 14B 15R
    /************************************************************************/

    T = rbt_insert(T,11);
    T = rbt_insert(T,7);
    T = rbt_insert(T,1);
    T = rbt_insert(T,2);
    T = rbt_insert(T,8);
    T = rbt_insert(T,14);
    T = rbt_insert(T,15);
    T = rbt_insert(T,5);
    T = rbt_insert(T,4); 

    T = rbt_insert(T,4); //重复插入测试
    rbt_print(T);

    /************************************************************************/
    /* 2    测试删除
    /*  
    /*操作  连续删除4个元素 rbt_delete(T,8);rbt_delete(T,14);rbt_delete(T,7);rbt_delete(T,11);
    /*输出  前序遍历 ：  2B  1B  5R  4B 15B
    /*      中序遍历 ：  1B  2B  4B  5R 15B
    /************************************************************************/

    rbt_delete(T,8);
    rbt_delete(T,14);rbt_delete(T,7);rbt_delete(T,11);

    rbt_delete(T,8);//删除不存在的元素
    rbt_print(T);

}

参考

https://blog.csdn.net/weixin_42295110/article/details/119539842

https://www.jianshu.com/p/94a1ce4128bd

http://blog.csdn.net/weewqrer/article/details/51866488