导语

算法是程序猿们必修的一门功课，它指：1.为解决某一问题定义的计算过程；2.是通过一个有限的指令序列集合对特定问题进行求解的一种计算执行描述。评估一个算法的优劣的方式是复杂度，今天来具体讲一讲时间复杂度的计算方法。

典型的时间复杂度函数和他们对应的时间如下图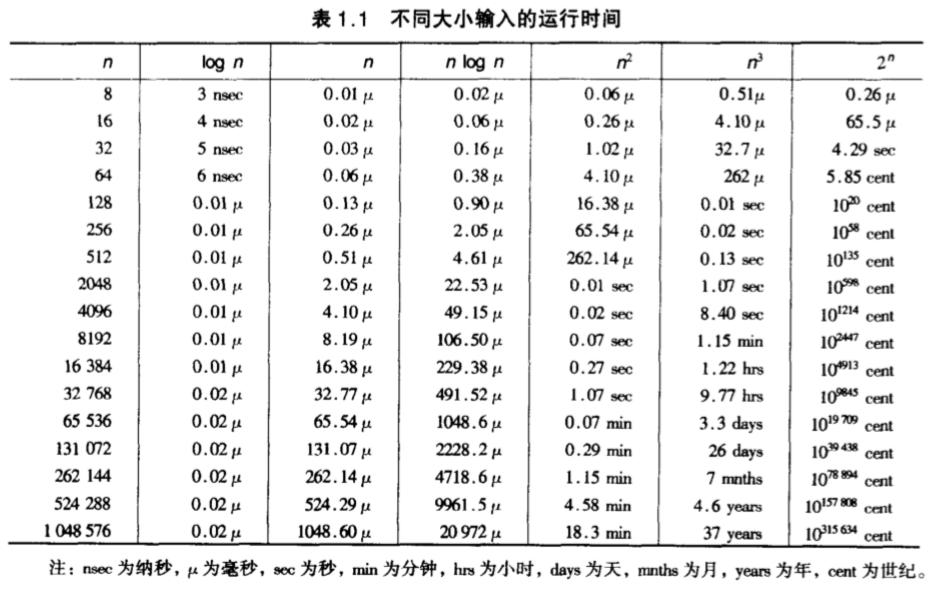

四个符号

O符号

假设：f(n)和g(n)是从自然数集到非负实数集里的两个函数
定义：如果存在正的常数C和自然数n0，使得当n≥n0时，有f(n)≤C·g(n)，则称函数f(n) 在n 充分大时有上有界，且g(n) 是它的一个上界，记做f(n)=O(g(n))
人话：当自变量大于某个值以后，f的函数值永远小于g的函数值乘以一个常数。
在这里，我们要明确的是，对于 $an^2+bn+c$，在n很大的时候，$a$、$bn+c$是不起作用的，也就是说，在进行阶的运算时，常系数、低的阶和常数项可以忽略。
只要用这种放缩放缩来放缩$n^2$ > nlogn > n > logn即可
重要性质：如果有
$\lim\limits_{n\to+\infty}\frac{f(n)}{g(n)}\not=0$
那么f(n)=O(g(n))

o符号

假设：f(n)和g(n)是从自然数集到非负实数集里的两个函数
定义：如果存在任意正的常数C和自然数n0，使得当n≥n0时，有0＜f(n)＜C·g(n)
人话：结合O符号看，这里主要的问题是要求对任意c都成立f(n)小于c·g(n)，也就是说要求g(n)和f(n)在数量级上有区分，当n趋于正无穷的时候f(n)相较于g(n)微不足道。在取极限的性质对比比较明显：
重要性质：如果有
$\lim\limits_{n\to+\infty}\frac{f(n)}{g(n)}=0$
那么f(n)=o(g(n))

Ω符号

假设：f(n)和g(n)是从自然数集到非负实数集里的两个函数
定义：如果存在正的常数C和自然数n0，使得当n≥n0时，有f(n)≥C·g(n)，则称函数f(n)在n充分大时有下有界，且g(n)是它的一个下界，记做f(n)= Ω(g(n))
人话：当自变量大于某个值以后，f的函数值永远小于g的函数值乘以一个常数。
和O符号就换汤不换药呗。
重要性质：如果有
$\lim\limits_{n\to+\infty}\frac{f(n)}{g(n)}\not=0$
那么f(n)=O(g(n))

θ符号

假设：f(n)和g(n)是从自然数集到非负实数集里的两个函数
定义：如果存在正的常数C和自然数n0，使得当n≥n0时，$C_1·$≤f(n)≤$C_2$·g(n)，则称函数f(n)在n充分大时有下有界，且g(n)是它的一个渐近确界，记做f(n)= θ(g(n))
人话：能同时整出来O和Ω就是θ
重要性质：如果有
$\lim\limits_{n\to+\infty}\frac{f(n)}{g(n)}=c$（其中c是一个大于零的常数）
那么f(n)=Ω(g(n))
换言之，O和Ω符号的极限可以是无穷，而θ符号必须是一个确定的数字。